Dalam dunia matematika dan ilmu komputer, matriks merupakan salah satu konsep dasar yang sangat penting. Matriks digunakan dalam berbagai aplikasi, mulai dari pemecahan sistem persamaan linier hingga transformasi grafik dalam komputer. Namun, banyak orang masih merasa bingung dengan berbagai jenis matriks dan bagaimana cara menggunakannya. Artikel ini akan membahas berbagai jenis matriks secara mendetail, memberikan contoh yang jelas, serta menjelaskan aplikasi praktis dari masing-masing jenis matriks.
Apa Itu Matriks?
Sebelum membahas jenis-jenis matriks, penting untuk memahami apa itu matriks. Matriks adalah kumpulan bilangan yang disusun dalam bentuk baris dan kolom. Setiap elemen dalam matriks dapat diakses dengan menggunakan indeks yang menunjukkan posisi baris dan kolomnya. Matriks sering kali digunakan untuk merepresentasikan data, melakukan perhitungan matematis, atau menyelesaikan sistem persamaan.
Jenis-Jenis Matriks
Berikut ini adalah beberapa jenis matriks yang umum digunakan beserta contohnya:
Matriks Identitas (Identity Matrix)
Definisi: Matriks identitas adalah matriks persegi dengan elemen diagonal utama (dari kiri atas ke kanan bawah) bernilai 1 dan elemen lainnya bernilai 0.

Aplikasi: Matriks identitas berfungsi sebagai elemen netral dalam operasi perkalian matriks, mirip seperti angka 1 dalam perkalian bilangan.
Matriks Nol (Zero Matrix)
Definisi: Matriks nol adalah matriks di mana semua elemennya bernilai 0.

Aplikasi: Matriks nol sering digunakan sebagai elemen netral dalam penjumlahan matriks dan dalam beberapa algoritma.
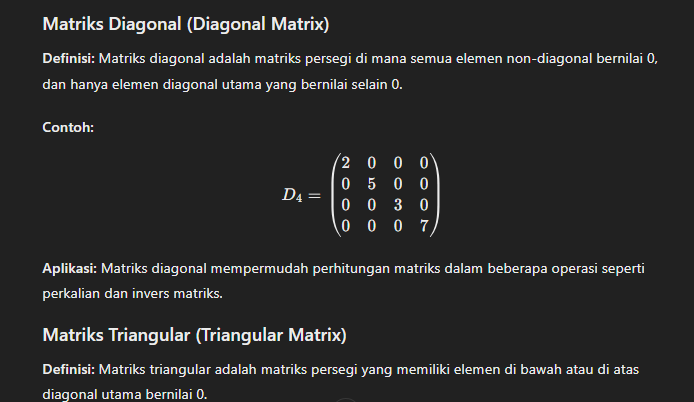
Matriks Diagonal (Diagonal Matrix)
Definisi: Matriks diagonal adalah matriks persegi di mana semua elemen non-diagonal bernilai 0, dan hanya elemen diagonal utama yang bernilai selain 0.

Aplikasi: Matriks diagonal mempermudah perhitungan matriks dalam beberapa operasi seperti perkalian dan invers matriks.
Matriks Triangular (Triangular Matrix)
Definisi: Matriks triangular adalah matriks persegi yang memiliki elemen di bawah atau di atas diagonal utama bernilai 0.
Matriks Triangular Atas (Upper Triangular Matrix)
Definisi: Matriks triangular atas adalah matriks persegi di mana semua elemen di bawah diagonal utama bernilai 0.

Matriks Triangular Bawah (Lower Triangular Matrix)
Definisi: Matriks triangular bawah adalah matriks persegi di mana semua elemen di atas diagonal utama bernilai 0.

Aplikasi: Matriks triangular sangat berguna dalam metode faktorisasi seperti faktorisasi LU yang digunakan dalam penyelesaian sistem persamaan linier.
Matriks Simetris (Symmetric Matrix)
Definisi: Matriks simetris adalah matriks persegi yang sama dengan transposenya. Artinya, elemen-elemen di sebelah kiri diagonal utama sama dengan elemen-elemen yang bersesuaian di sebelah kanan diagonal utama.
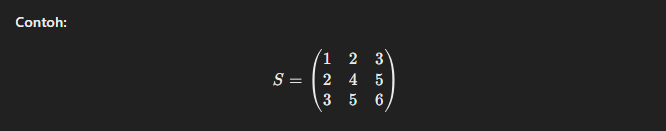
Aplikasi: Matriks simetris sering digunakan dalam aljabar linier dan statistik, termasuk dalam metode untuk optimasi dan analisis data.

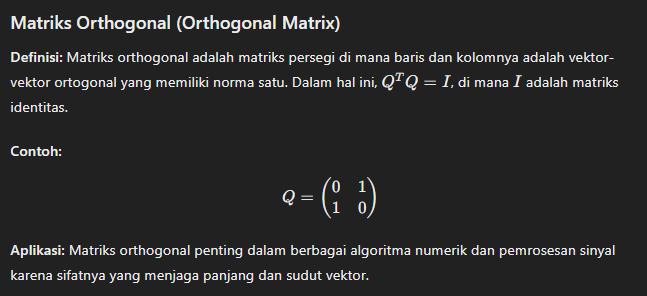

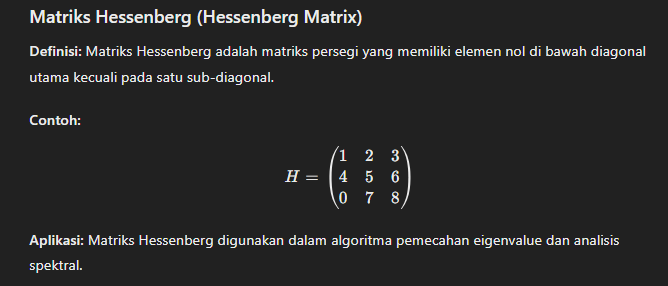

Contoh Kasus dalam Berbagai Bidang
Dalam Ilmu Komputer
Matriks digunakan dalam berbagai algoritma komputer, termasuk grafik komputer dan pemrosesan gambar. Sebagai contoh, matriks transformasi digunakan untuk rotasi, translasi, dan skala objek dalam grafik komputer.
Dalam Statistik
Matriks kovarians, yang merupakan matriks simetris, digunakan untuk menggambarkan hubungan antara variabel dalam analisis multivariat. Ini membantu dalam memahami pola dan struktur data.
Dalam Teknik
Dalam teknik elektro dan kontrol sistem, matriks digunakan untuk analisis sistem dinamis dan desain kontrol. Faktorisasi matriks, seperti faktorisasi LU, memainkan peran penting dalam simulasi dan optimasi.
Kesimpulan
Memahami berbagai jenis matriks dan aplikasinya sangat penting dalam matematika, ilmu komputer, dan berbagai bidang lainnya. Dengan pengetahuan tentang matriks identitas, diagonal, triangular, simetris, skew-simetris, orthogonal, dan lainnya, kita dapat lebih efektif dalam memecahkan masalah dan menerapkan konsep matematika dalam praktek nyata.
Semoga panduan ini membantu Anda memahami dan menggunakan matriks dengan lebih baik. Jangan ragu untuk menggali lebih dalam setiap jenis matriks dan aplikasinya untuk memanfaatkan potensi penuh dari alat matematika ini.